A robust mechanism for Kanban board column indexing
A human-readable indexing approach that can accommodate user-configurable sort orders.
Contents:
Notes
This post was updated on 2025-03-31 to reflect changes made to the package in January 2025. These changes brought the
package in line with the original approach used for the Anneal project, and addressed an issue with the
compute_intermediate_index function that was introduced when packaging the utility for external consumption.
TL;DR
We used strings to track the positions of cards in a Kanban board column. This allowed for easy insertions, deletions, and reordering of cards without the need for reindexing. The approach was designed to be human-readable, and should be able to scale to handle a large number of cards.
Background
Kanban boards are ubiquitous. They’re a standard tool in project management, and I imagine that anyone arriving at this post will have, more likely than not, used one before. Like a glorified to-do list, these boards are used to track progress on tasks or projects, and are typically divided into columns that represent different stages of completion.
Physical versions are often used on machine shop floors and in production offices, and can be as simple as a whiteboard littered with Post-it notes. When someone makes some progress on a given piece of work, they pick up the corresponding note and move it from one status column to the next.
The digital versions are found all over the place now, too. I suspect these probably have their origins in software developers importing tools from the manufacturing world, with the contagion spreading onwards from there. There’s a long, long list of products out there that offer these; I can think of at least ten without going to Google:
- Trello,
- Jira,
- Asana,
- Monday,
- Linear,
- GitLab,
- Wrike,
- Notion,
- Miro,
- ClickUp.
On the Anneal project, I wanted to offer nice workflow management on top of the CAD and drawing review and various other more vertical-specific tools, so the Kanban system ended up being one of the first features I built.
It was a more interesting job than I’d anticipated, and I thought it might be worth writing up and sharing.
I was somewhat hesitant to share the inner workings of the approach at first but, on reflection, figured there’s really no downside to it. Given that the actual user-facing functionality is effecitvely commoditised, and that end users almost certainly don’t care at all about how the card ranking and sorting works under the hood, I thought this might be interesting to anyone building a similar system.
Requirements
Building this as a one man band, I didn’t run through a formal requirements process, but the requirements I had in my head were fairly simple:
- The system should support a configurable number of columns.
- It should be able to handle a large number of cards within each column without significant performance issues.
- Users should be able to sort cards within a column in any order they like, and this order should be persisted.
- The sorting should support both manual drag-and-drop reordering and automatic sorting based on criteria like due date or priority.
- All operations should be performant, avoiding noticeable delays or UI freezes.
Possible solutions
Before writing any code, I mulled over a few possible approaches. At first glance, this seems like an easy one… it’s just a list of cards in some specific order. My initial thoughts were a that list of integer indices or a linked list should do it, and while that isn’t wrong, it’s not quite right either.
If I’d been building a single-user desktop app, I think the linked list is basically perfect. You can insert and delete items in constant time, and you can traverse the list in linear time. It’s a good fit—simple and efficient. However, I was building this for a multi-user web app, and the list of cards in a column could be very long. We also needed to store the index of each card not just in memory, but in a database, and there might be multiple users interacting with the same column at the same time.
So it needed a bit more thought. Working through the options I could think up, we basically have:
1. Linked list
This is probably the most obvious solution. We could implement the column as a linked list, where each card maintains a reference to the card after (and/or before) it.
The broad idea here is to arrive at the following, with each card holding some pointer to the next card.
Before insertion:
[C1] -> [C2] -> [C3] -> [C4] -> [C5]
After inserting C6 between C2 and C3:
[C1] -> [C2] -> [C6] -> [C3] -> [C4] -> [C5]
Practically, that means something more like this:
Before insertion:
Card: [C1] [C2] [C3] [C4] [C5]
| | | | |
Next: C2 C3 C4 C5 NULL
After inserting C6 'between' C2 and C3:
Card: [C1] [C2] [C3] [C4] [C5] [C6]
| | | | | |
Next: C2 C6 C4 C5 NULL C3
Pros:
- Efficient insertions and deletions.
- Relatively straightforward to implement.
Cons:
- All operations require changes to more than one record.
- Column order is not immediately human-readable; you basically have to traverse the list to see the order of its items.
- This also makes it a bit of a pain to view things in a database client. You can’t just use an
ORDER BYclause to get the cards in the right order; you have to pull them all out and then sort them first.
- This also makes it a bit of a pain to view things in a database client. You can’t just use an
2. Integer indexing
The simplest approach I could think of was to use integer indices for each card. You assign a unique integer to each
card, and the order of the cards is determined by these indices: card 1 comes before card 2, and so on. When you add
a new card, you increment the indices of all the cards that come after it. When you move a card, you update its index
and reindex the cards around it.
With cards C1, C2, C3 etc., that looks something like this:
Before insertion:
Card: [C1] [C2] [C3] [C4] [C5]
| | | | |
Index: 1 2 3 4 5
After inserting C6 between C2 and C3:
Card: [C1] [C2] [C6] [C3] [C4] [C5]
| | | | | |
Index: 1 2 3 4 5 6
Pros:
- Incredibly simple to implement and understand.
- Plays nicely with databases and sorting operations.
Cons:
- Requires reindexing when inserting or moving cards.
- Likely to be slow for large numbers of cards if new values must be assigned.
For large boards, that reindexing sounds like it could be a nightmare. You could make one relatively simple change by shuffling a card around, and suddenly find you’re having to lock the whole column while you reindex everything. If you had 300 cards in a column, that could be a noticeable delay.
3. Fractional indexing
This method uses floats instead of integers for the index values, allowing for insertions by choosing a number between two existing indices. The idea is pretty simple, and straightforward enough to illustrate:
Before insertion:
Card: [C1] [C2] [C3] [C4] [C5]
| | | | |
Index: 1.0 2.0 3.0 4.0 5.0
After inserting C6 between C2 and C3:
Card: [C1] [C2] [C6] [C3] [C4] [C5]
| | | | | |
Index: 1.0 2.0 2.5 3.0 4.0 5.0
Unfortunately, this solution leaves you open to bumping into floating-point precision issues. For example, if you have a column that tracks a very large number of cards which have been added one after another, you end up having less and less ability to insert new cards between them, as you’re basically trading off your capacity to represent number magnitude for precision.
This gives a nice illustration of the distribution of floating point numbers:
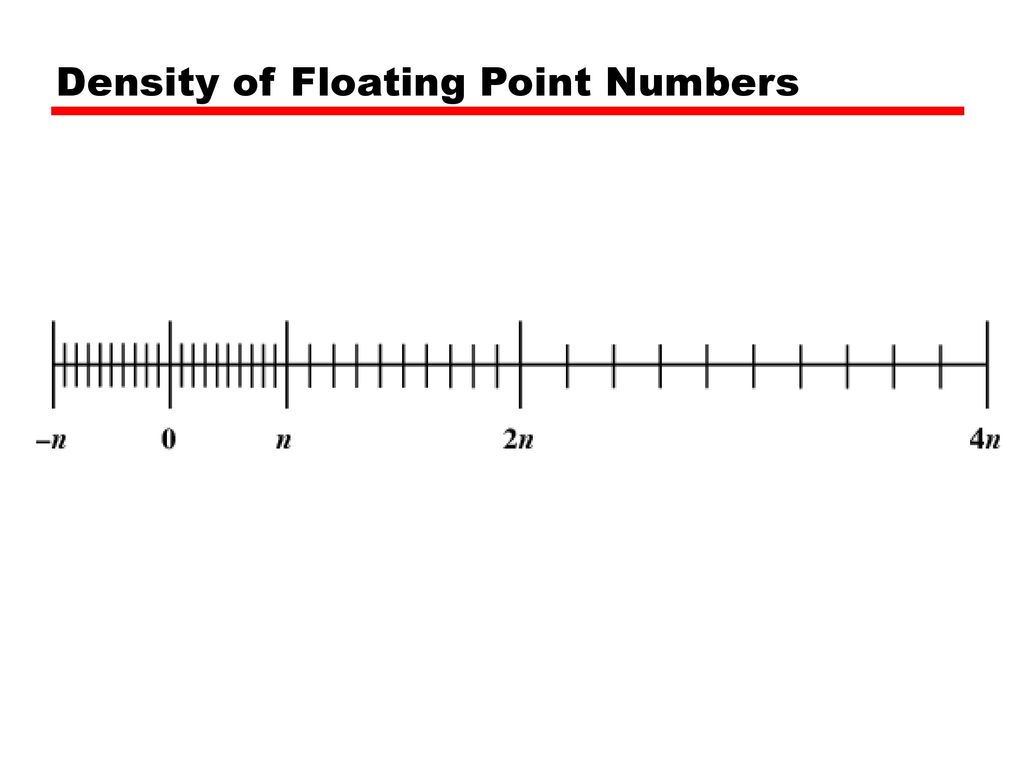
Expressible Numbers.
However, unless you hit unicorn scale and have some slightly deranged users, I think it’s probably pretty unlikely that you’d ever hit this kind of issue in practice. That said, as an example of the sort of issue you could encounter, let’s pretend we’re using a minifloat-style 4-bit floating-point system. Obviously nobody would ever actually do this, but it highlights some of the potential issues. Our spec will be:
- 1 bit for the sign.
0for positive,1for negative.
- 2 bits for the exponent.
00for the representation of subnormals.01represents 2^0, so 1.10represents 2^1, so 2.11will be reserved for special values:InfandNaN.
- 1 bit for the mantissa.
0represents.0in binary; 0.1represents.1in binary; 0.5.
This system actually has a small enough range of possible values that we can enumerate them:
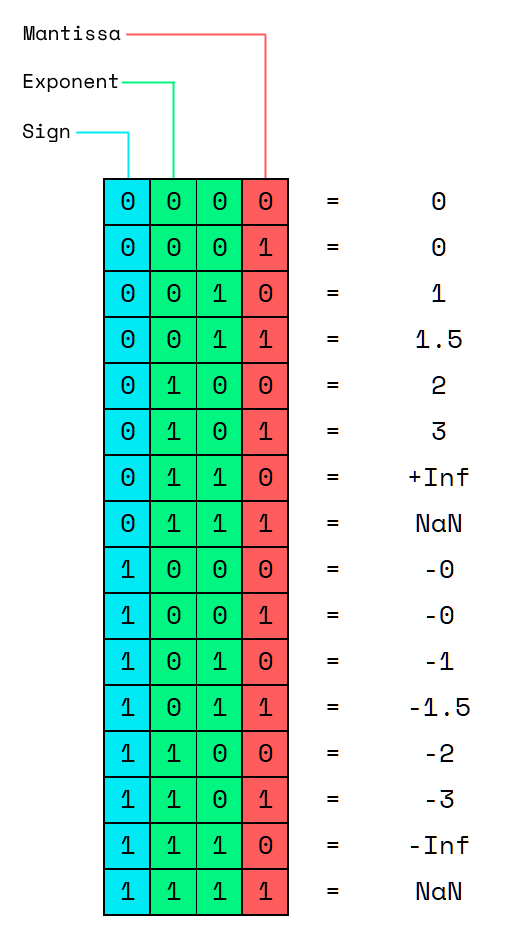
We can even present this as a matrix, pairing off the bits:
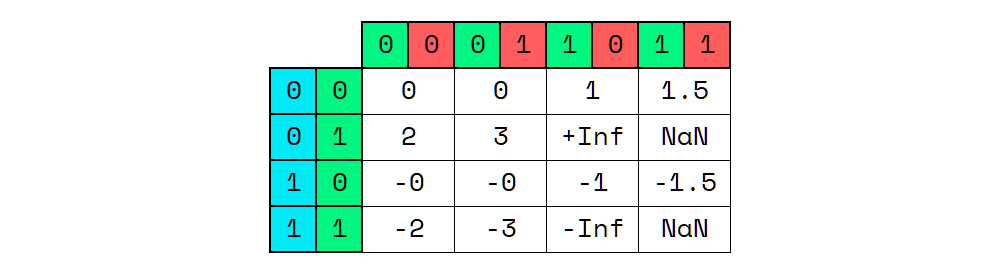
In our Kanban scenario, this setup would start to cause problems pretty quickly. For example, if we had cards C1 and
C2 with indices at 1 and 2, you could insert a new card, C3, between them, and it would be assigned the index
1.5.
If you then wanted to move C2 between C1 and C3, you’d have to recompute a full set of indices—because there are
no values between 1 and 1.5 that can be represented in this system; we’ve exhausted the unique values that can be
represented in the range we need:
Initial state:
Card: [C1] [C2]
| |
Index: 1.0 2.0
New card insertion:
Card: [C1] [C3] [C2]
| | |
Index: 1.0 1.5 2.0
Reordering
Card: [C1] [C2] [C3]
| | |
Index: 1.0 ☠️ 1.5
As I said above, I think the likelihood of this causing issues in the real world, even with single precision floats, is
extremely low. Doing some back-of-the-envelope analysis, I think it should be possible to squeeze $2^{23} - 2$ unique
values between 1 and 2 with a 32-bit float—that’s north of 8 million. However, if you had a column with a million
cards in it such that you were trying to squeeze new cards between 1000000 and 1000001, you get a lot less
headroom: just $2^{4} - 2$ possible values; 14.
At the time, fear of bumping into these sorts of issues was enough to make me want to keep looking for alternatives. However, given that I didn’t actually do this level of analysis until writing this post, I now think the floating point system is probably not a bad solution—and you can always switch to double precision floats if you find usage going haywire.
Pros:
- Allows for easy insertion between any two items.
- No immediate need for reindexing.
- Again, plays nicely with databases and sorting operations.
Cons:
- Limited precision can lead to index exhaustion.
- Possible inter-card range not uniform across the full range of possible index values.
- Potential for rounding errors.
- May require occasional rebalancing of indices.
4. Gap buffer
A gap buffer maintains empty spaces in the index range, allowing for efficient insertions. This is the sort of thing I’ve seen with some item numbering systems in the engineering world, where you might increment by 10s or 100s to allow for later insertions that you can just slot in between the existing items.
You might adopt something like this with a standard operating procedure document where the steps are numbered, but where you want to guard against having to renumber everything in the event you need to add more detail or modify a process later.
Before insertion:
Card: [C1] [C2] [C3] [C4] [C5]
| | | | |
Index: 10 20 30 40 50
After inserting C6 between C2 and C3:
Card: [C1] [C2] [C6] [C3] [C4] [C5]
| | | | | |
Index: 10 20 25 30 40 50
Here, the problem is that you’re still going to have to reindex everything if you run out of space in your buffer. If that ends up happening frequently, you’re back to having broadly the same problem set as with integer indexing.
Pros:
- Efficient for localised insertions and deletions.
- Easy to implement.
- Plays nicely with databases and sorting operations.
Cons:
- May require reindexing when inserting or moving cards.
- Could be slow for large numbers of cards if reindexing.
5. Tree-based structures
This is definitely at the limit of my working knowledge of data structures, given that I’m a mechanical engineer by training, but a self-balancing tree structure like a B-tree or Red-Black tree might also fit the bill. These structures allow logarithmic time lookups, insertions, and deletions, and can be used to maintain a sorted list of items—which is exactly what we’re after here.
Broadly, the idea is to maintain a tree structure where each node contains a set number of keys and pointers to child nodes. Nodes can fall into two categories: internal nodes, which contain keys that guide search, and leaf nodes, which are at the extreme ends of the tree and contain the actual items (or pointers to them).
Trying to visualise this, we can imagine a tree structure where the internal nodes use buffer gap style integer keys, and where the leaf nodes contain some reference to our cards. Consdiering our usual insertion example, that looks something like:
Before insertion:
[20]
______/ \______
/ \
[10,15] [30,40]
/ | \ / | \
[C1] [C2] [C3] [C4] [C5] [ ]
After inserting C6 (with key 25):
[20,30]
_______/ | \_______
/ | \
[10,15] [25] [40]
/ | \ | / \
[C1][C2][C3] [C6] [C4][C5]
Some general notes on this:
- In this example, each internal node can hold up to 2 keys and 3 children.
- Keys in a node are always in ascending order.
- Children to the left of a key have values less than the key.
- Children to the right of a key have values greater than or equal to the key.
Then considering the actual insertion process, before insertion we see:
- Root node has key 20.
- Left child has keys 10 and 15, with cards C1, C2, C3 in its leaf nodes.
- Right child has keys 30 and 40, with cards C4, C5 in its leaf nodes.
While after inserting C6 (with key 25):
- Root node now has keys 20 and 30.
- Left child remains unchanged.
- Middle child is created with key 25 and card C6.
- Right child now only has key 40 with cards C4 and C5.
Note that we’ve rearranged the tree to keep its ‘height’ the same, which is a key feature of these self-balancing trees.
Pros:
- Efficient for large numbers of items.
- Good performance for insertions, deletions, and lookups.
Cons:
- More complex to implement—I’d have to dig into how you could store this in a database.
- Overkill for smaller lists.
- Not immediately human-readable.
6. Lexicographic indexing
The final contender is the sort of thing that would probably be the first possible solution thought up by anyone who’s never used a computer before: just make it alphabetical.
In this particular case, the concept is incredibly similar to the fractional indexing system, but instead of using floating point numbers, we use strings. The pattern I thought up here was to use a 26-character alphabet where each card is assigned an index that’s just a string of characters. The concept basically works like this:
- We use a 26-character alphabet (
A-Z) to generate indices. - Each card’s position is represented by a string of these characters.
- The lexicographic (dictionary) order of these strings determines the card’s position.
- When inserting a new card between two existing ones, we generate a new index that lexicographically falls between the two surrounding indices.
Practically, that means:
- We would start with the letter
B. When the first card is assigned to a column, it’s given the indexB.- This is so that new cards can be inserted ‘before’ the first card.
- When a new card is added, it’s given the next letter in the alphabet. After
Bwould comeC, thenD, and so on. - If you wanted to insert a new card between
BandC, you would see that there’s no full letters available, so you you need to add another character. For maximum flexibility, you want this character to be bang in the middle of the alphabet, so you’d addMto getBM. - If you wanted to insert a card before
B, you would increment the number of characters by one, and then go for the last letter in the alphabet,Z, to getAZ.
This pattern basically scales ~forever. You can keep adding characters to the index string to keep inserting new cards between existing ones, and you can keep adding new cards to either end of the list as well.
Before insertion:
Card: [C1] [C2] [C3] [C4] [C5]
| | | | |
Index: B C D E F
After inserting C6 between C2 and C3:
Card: [C1] [C2] [C6] [C3] [C4] [C5]
| | | | | |
Index: B C CM D E F
After inserting C7 before C1:
Card: [C7] [C1] [C2] [C6] [C3] [C4] [C5]
| | | | | | |
Index: AZ B C CM D E F
Pros:
- Allows for virtually unlimited insertions without reindexing.
- Preserves order and allows easy reordering.
- Simple string comparisons for sorting.
Cons:
- Slightly more complex to implement than simple integer indexing.
- Potential for long index strings in extreme cases.
Picking a winner
On balance, I felt that the lexicographic indexing approach was the best. By choosing that pattern, the ordering will be immediately human readable, we’ll never have to reindex a column, we have no fear of precision issues, and it should basically scale forever.
I’m also a Postgres fanboy, and it felt like a natural fit for the flexible
text column type in Postgres:
In addition, PostgreSQL provides the
texttype, which stores strings of any length. Although the type text is not in the SQL standard, several other SQL database management systems have it as well.
The downside is that it’s slightly more work than a float or integer based approach, but really not by much.
Building a Python package
Almost all of our backend was written in Python, so I set about putting together a library we could call on to handle the indexing. I’ve packaged this up, made it open source, and published it to PyPI:
However, the structure of the functional code is incredibly simple, so I can actually share the contents here. It really boils down to two files:
alphabet_indexer.py: contains a class definition that handles the bidirectional mapping between characters in the alphabet and their correspdonding indices in that alphabet, alongside giving easy access to special values and handling some validation.main.py: handles all of the actual logic that will be called on, e.g. getting the initial index for a card going into an empty column, computing the index required to insert a card between two existing cards etc.
alphabet_indexer.py
class AlphabetIndexer:
"""
A class that provides indexing functionality for a given alphabet.
This class creates a bidirectional mapping between characters in the alphabet
and their corresponding integer indices. It also provides utility methods
for converting between characters and indices, and properties for accessing
special characters in the alphabet.
The alphabet is expected to be a sorted string of unique characters.
"""
def __init__(self, alphabet: str):
"""
Initialize the AlphabetIndexer with a given alphabet.
Args:
alphabet (str): A sorted string of unique characters representing the alphabet.
Raises:
ValueError: If the provided alphabet is not sorted or contains duplicate characters.
"""
# Verify that the alphabet is sorted and contains unique characters
if list(alphabet) != sorted(set(alphabet)):
raise ValueError(
"The provided alphabet must be sorted and contain unique characters."
)
# Create bidirectional mappings between characters and their indices
self.char_to_int = {char: i for i, char in enumerate(alphabet)}
self.int_to_char = {i: char for i, char in enumerate(alphabet)}
self.alphabet = alphabet
def to_int(self, char) -> int:
return self.char_to_int[char]
def to_char(self, i) -> str:
return self.int_to_char[i]
@property
def start(self) -> str:
return self.alphabet[0]
@property
def end(self) -> str:
return self.alphabet[-1]
@property
def midpoint(self) -> str:
"""
Get the middle character of the alphabet.
For even-length alphabets, returns the character to the left of the midpoint.
For odd-length alphabets, returns the exact midpoint character.
Returns:
str: The middle character of the alphabet.
"""
mid_index = (len(self.alphabet) - 1) // 2
return self.alphabet[mid_index]
main.py
"""
This module implements a lexicographic indexing system for (user configurable) ordered
collections, such as a column on a Kanban board.
It uses a base-26 system (A-Z) to generate indices, allowing for ~infinite
insertions between any two existing indices without the need for reindexing.
The system avoids floating-point precision issues by using string comparisons—also
making the indices readily human-readable.
Key features:
- Indices are strings composed of characters A-Z
- Lexicographic ordering determines item placement
- New indices are generated at the midpoint between existing indices
- The default range is (A, Z], allowing insertions before the first item
Example: Between indices "B" and "C", a new item would receive index "BM".
"""
from kanban_indexer.alphabet_indexer import AlphabetIndexer
# Define our alphabet and create AlphabetIndexer map instance.
ALPHABET = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
ALPHA_MAP = AlphabetIndexer(ALPHABET)
ALPHABET_START = ALPHA_MAP.start
ALPHABET_END = ALPHA_MAP.end
ALPHABET_MIDPOINT = ALPHA_MAP.midpoint
# Set our first index value for a new/empty column.
INIT_ORDINAL = ALPHA_MAP.to_int(ALPHABET_START) + 1
INIT_INDEX = ALPHA_MAP.to_char(INIT_ORDINAL)
def get_new_index() -> str:
"""
Retrieves an initial index for a new column.
Returns:
str: The new index.
"""
return INIT_INDEX
def validate_index(index: str) -> None:
"""
Validates the given index string.
Args:
index (str): The index string to be validated.
Raises:
ValueError: If the index contains any character that is not in the range
[ALPHABET_START, ALPHABET_END] or if the index ends with
ALPHABET_START.
Returns:
None
"""
# Index is invalid if any character is not in [ALPHABET_START and ALPHABET_END].
if any(char not in ALPHA_MAP.char_to_int for char in index):
raise ValueError(
f"Invalid index: '{index}'. "
f"Characters must be in range ('{ALPHABET_START}', '{ALPHABET_END}']."
)
# Index is invalid it ever ends with ALPHABET_START.
if index.endswith(ALPHABET_START):
raise ValueError(
f"Invalid index: '{index}'. " f"Index cannot end with '{ALPHABET_START}'."
)
def compute_midpoint(ordinal_a: int, ordinal_b: int) -> int:
"""
Computes the midpoint between two values.
Args:
ordinal_a (int): The first ordinal value.
ordinal_b (int): The second ordinal value.
Returns:
int: The midpoint between the two values.
"""
return (ordinal_a + ordinal_b) // 2
def compute_intermediate_index(index_before: str, index_after: str):
"""
Computes the intermediate index between two given indices using an expansion flag approach.
Args:
index_before (str): The index of the item 'before' the target position.
index_after (str): The index of the item 'after' the target position.
Returns:
str: The computed intermediate index.
Raises:
ValueError: If the input indices are not valid.
"""
# Validate input indices.
validate_index(index_before)
validate_index(index_after)
# Flip order if necessary.
if index_before > index_after:
index_before, index_after = index_after, index_before
intermediate_index = ""
expand_flag = False
max_length = max(len(index_before), len(index_after))
for i in range(max_length):
# Get the ordinal values, using ALPHABET_START as default for padding.
lo = (
ALPHA_MAP.to_int(index_before[i])
if i < len(index_before)
else ALPHA_MAP.to_int(ALPHABET_START)
)
# For the high value, use ALPHABET_END.
hi = (
ALPHA_MAP.to_int(index_after[i])
if (i < len(index_after) and not expand_flag)
else ALPHA_MAP.to_int(ALPHABET_END)
)
if lo == hi:
intermediate_index += ALPHA_MAP.to_char(lo)
elif (hi - lo) > 1:
intermediate_index += ALPHA_MAP.to_char(compute_midpoint(lo, hi))
expand_flag = False
return intermediate_index
else:
intermediate_index += ALPHA_MAP.to_char(lo)
expand_flag = True
if expand_flag:
intermediate_index += ALPHABET_MIDPOINT
return intermediate_index
def compute_preceding_index(index: str) -> str:
"""
Returns the preceding index value based on the given index.
Args:
index (str): The index value.
Returns:
str: The preceding index value.
Raises:
ValueError: If the index is not valid.
"""
validate_index(index)
# Iterate backwards through the string.
for i in range(len(index) - 1, -1, -1):
cur_char_ordinal = ALPHA_MAP.to_int(index[i])
if cur_char_ordinal > INIT_ORDINAL:
# Decrement least significant character, e.g. CC -> CB.
return index[:i] + ALPHA_MAP.to_char(cur_char_ordinal - 1) + index[i + 1 :]
# If we've reached here, all characters were at INIT_ORDINAL already.
# Expand string and replace previously least significant char,
# e.g. BB -> BAZ.
return index[:-1] + ALPHABET_START + ALPHABET_END
def compute_succeeding_index(index: str) -> str:
"""
Returns the succeeding index based on the given index.
Args:
index (str): The index to find the succeeding index for.
Returns:
str: The succeeding index.
Raises:
ValueError: If the index is not valid.
"""
validate_index(index)
if index[-1] == ALPHABET_END:
# If the last character is Z, append INIT_INDEX.
return index + INIT_INDEX
# Otherwise, increment the last character.
return index[:-1] + ALPHA_MAP.to_char(ALPHA_MAP.to_int(index[-1]) + 1)
Walkthrough
For compute_intermediate_index:
- Validate both input indices to ensure they’re in the correct format.
- If
index_beforeis lexicographically greater thanindex_after, swap them to ensure correct ordering. - Initialise an empty string,
intermediate_index, to store the result. - Set
expand_flagtoFalse. This flag will indicate when we need to expand with an additional character. - Find the maximum length between the two input indices.
- For each character position up to the maximum length:
- Get the ordinal values for each index at this position, using
ALPHABET_STARTas the default for padding the shorter index. - For the higher value, use
ALPHABET_ENDif we’re already in expansion mode. - If both ordinals are equal, add this character to our intermediate index.
- If the difference between ordinals is greater than 1:
- Compute the midpoint between them and add that character to the intermediate index.
- Turn off the expansion flag and return the result immediately.
- If the difference is exactly 1:
- Add the lower ordinal character to the intermediate index.
- Set the expansion flag to
Trueto indicate we need to expand to the next position.
- Get the ordinal values for each index at this position, using
- If we finish the loop with the expansion flag still set, append the alphabet’s midpoint character.
Then, for compute_preceding_index:
- Validate the input index.
- Iterate through the index string from right to left:
- Convert each character to its ordinal value.
- If the ordinal is greater than the initial ordinal:
- Decrement this character by one.
- Return the modified index.
- If no character could be decremented (all at minimum value):
- Remove the last character.
- Append the start of the alphabet followed by the end of the alphabet.
Finally, for compute_succeeding_index:
- Validate the input
indexusing thevalidate_index()function. - Check if the last character of the
indexis equal toALPHABET_END.- If the last character is
ALPHABET_END, appendINIT_INDEXto theindex.
- If the last character is
- If the last character is not
ALPHABET_END:- Convert the last character of the
indexto its corresponding integer usingALPHA_MAP.to_int(). - Increment the integer by one.
- Convert the incremented integer back to a character using
ALPHA_MAP.to_char(). - Return the original
indexwith the incremented character replacing the last character
- Convert the last character of the
Limitations
While this approach offers some attractive features in terms of flexibility and scalability, there are some limitations to be aware of:
- Performance and speed.
- Since lexicographic indexing requires calculation at a layer above the database (in this case, Python), it may introduce some latency in larger systems, especially with frequent inserts or updates in real-time collaborative environments.
- String growth.
- Over time, as more items are inserted between existing indices, the string representations can grow longer. This could slightly impact storage efficiency and sorting performance if the number of items in a column grows large and many inserts happen between two close indices.
- Collisions.
- While the indexing system is designed to reduce the likelihood of index collisions, theoretically, edge cases could emerge in large or highly active boards where many items are inserted at once in the same position.
- Since we then sort alphabetically, this shouldn’t cause any major headaches, but I can imagine there basically being some non-deterministic behaviour in the ordering of items that have the same index.
- Database overhead.
- Since the indexing is managed in Python and the indices are stored as strings, performance in a database context (e.g., during sorting and retrieval) may be worse than with numeric types. Direct integer-based or float-based comparisons are typically more efficient in database operations.
Conclusion
The lexicographic indexing approach provides a robust solution for managing card indices on a Kanban board. It eliminates the need for costly reindexing operations, should be able to handle large numbers of insertions between items, and ensures a human-readable order at the end of it. Although there are some trade-offs, such as possibly increasing string length over time and a reliance on Python for computation, we never encountered any problems with this method on the Anneal production environment.
For most use cases, this approach should offer a decent balance of simplicity, efficiency, and scalability.